The industrial revolution caused an explosion in technology and economic growth. At the same time, though, it also led to major societal and environmental problems, even to the point of potentially causing our own demise. To solve these problems, it will be helpful to understand better how we got here in the first place. A new theory provides an alternative but mathematically precise explanation of technological evolution by modeling it as a process of combinatorial innovation.
Technological Evolution
Three million years ago, our ancestor Australopithecus used tools that were commonly found in the environment, including stones, sticks, and bones. Over time, these tools were slowly improved by deliberately shaping them into cutters, diggers, scrapers, crushers, and so on, but they remained relatively simple. The diversity of these tools was probably on the order of a dozen or two.
Around 300,000 years ago, early humans like Homo heidelbergensis attached a stone tool such as a hand axe to a stick using a piece of string made from dried flax or other plant material, resulting in a hafted axe. Similar technological innovations were made as well, such as spears, hammers, fishing gear, and so on. The diversity of tools was now probably on the order of a hundred.

Roughly 12,000 years ago, just after the end of the last ice age, modern humans started practicing agriculture. This required a whole new set of tools including plows, wheel barrows, millstones, and so on. As a consequence, more technological innovations were made that led to another significant increase in the diversity of tools, now probably on the order of a thousand.
Around 250 years ago, the invention of an efficient steam engine fueled the industrial revolution, which quickly led to an explosion in new technologies. The first flight took place at the beginning of the 20th century, and less than 70 years later humans went to the moon. Today, we have an endless range of sophisticated technologies, from paperclips, multi-tools, and conveyor belts, to trains, computers, and the international space station.
Combinatorial Innovation
Technological evolution, as just described, is largely combinatorial in nature. New technologies often consist of innovative and improved combinations of currently existing technologies. This holds for tools used hundreds of thousands of years ago as well as technology from the industrial revolution and beyond.
For example, one of the first truly combinatorial innovations was the hafted axe mentioned above. It was a combination of simple tools that were already used individually for various purposes. However, this combination gave rise to a new and innovative tool that allowed early humans to perform existing tasks more efficiently, or even perform additional tasks not possible before.
With modern technology it is not always immediately obvious which earlier technologies were combined to make the new technology. However, going back to the very first versions of such modern technologies often reveals this more clearly. For example, the very first passenger trains were a combination of a steam locomotive as already used in coal mines and passenger carriages that were originally drawn by horses.
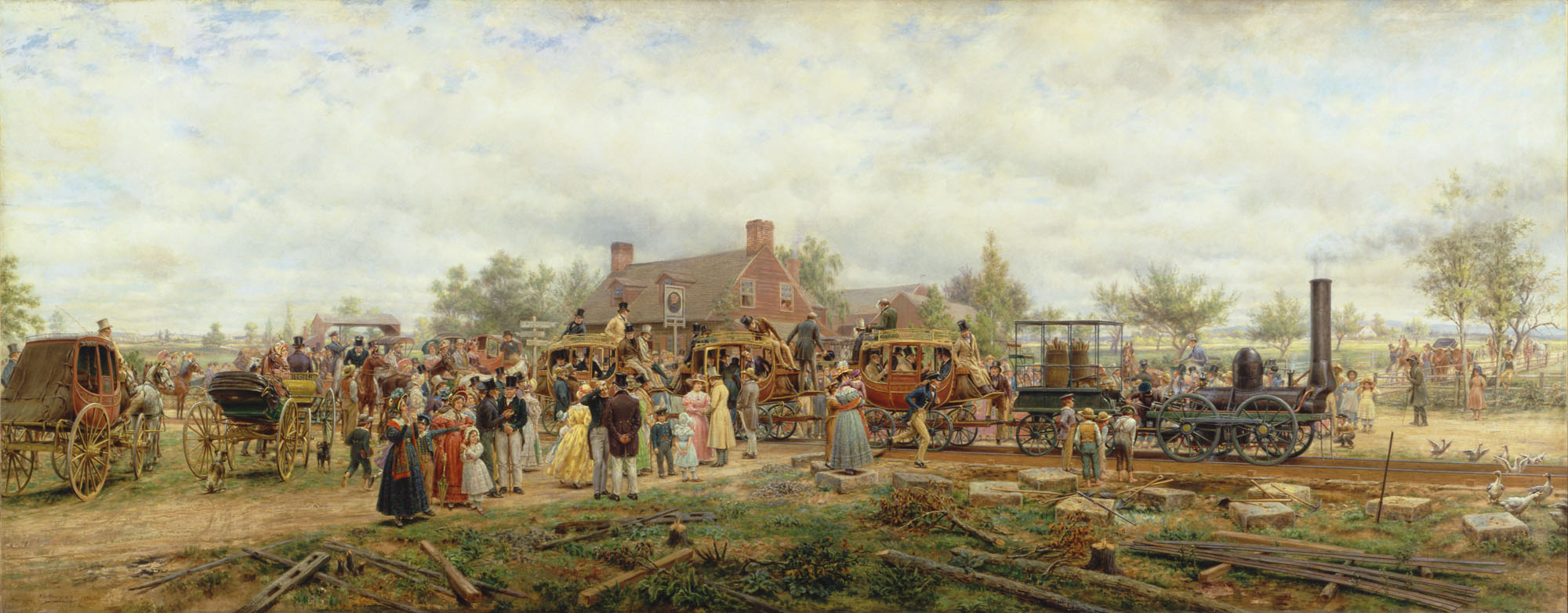
The above image is of a painting by the American artist Edward Henry called The First Railroad Train on the Mohawk and Hudson Road. The train carriages were still exactly the same as the original horse-drawn ones (as in the left of the painting), simply put on rails. In fact, some of the passengers were even still sitting on the outside of the carriages!
Theory of the Adjacent Possible
When there are only a few current technologies, or tools, there are also relatively few possible combinations to create new technologies. However, when the number of existing technologies increases, the number of possible combinations increases even faster. Of course not all of these new combinations might be useful in any way, but even if just a small fraction of them are, there is an ever expanding space of possibilities for new inventions and innovations over time.
This is what the theory of the adjacent possible (TAP), as originally proposed by theoretical biologist Stuart Kauffman, is all about. At any moment there is an "adjacent possible" of all the potential new combinations of currently existing technologies, and with every actual innovation this adjacent possible grows larger, giving rise to even more (potential) new combinations. Hundreds of thousands of years ago, trains were not in the adjacent possible yet, but hafted axes were. The invention of the steam engine in the 18th century increased the adjacent possible significantly, which then also included locomotives and, subsequently, trains.
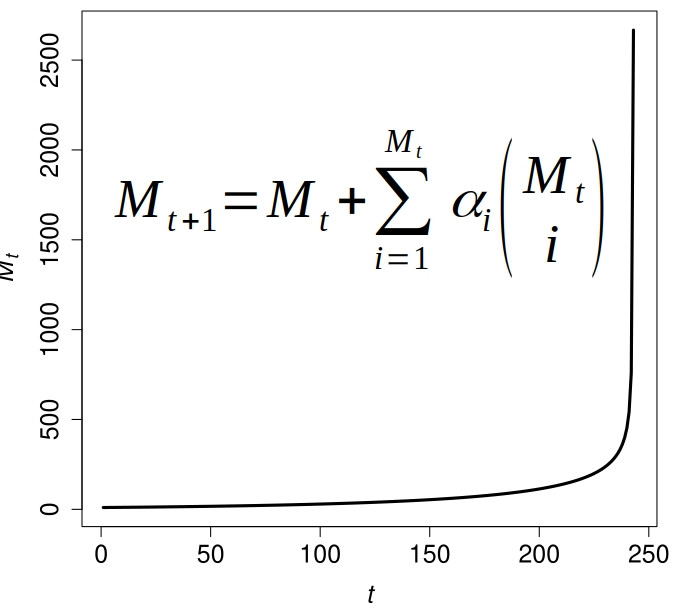
The core idea of TAP is captured in a simple mathematical equation. Consider the number of technologies Mt existing at a given time step t. The TAP equation then states that the number of technologies Mt+1 at the next time step t+1 is the number of current technologies Mt plus a certain number of new technologies that are formed by combinations of the currently existing technologies. Such a new technology can be based on a single currently existing technology (perhaps an improved version of it), or on a combination of two existing technologies (such as a steam locomotive and a horse carriage), or three existing technologies (a stick, a stone, and a string), or any number up to Mt. Finally, each of these possible combinations of current technologies has a certain probability of actually being tried out and resulting in a useful new technology. (For the interested reader, the actual equation is displayed in the image at the beginning of this article.)
Given certain values for these probabilities, and a small number of initial technologies M0, the TAP equation produces a sequence of values for Mt (vertical axis) over time (horizontal axis) as shown in the following image.
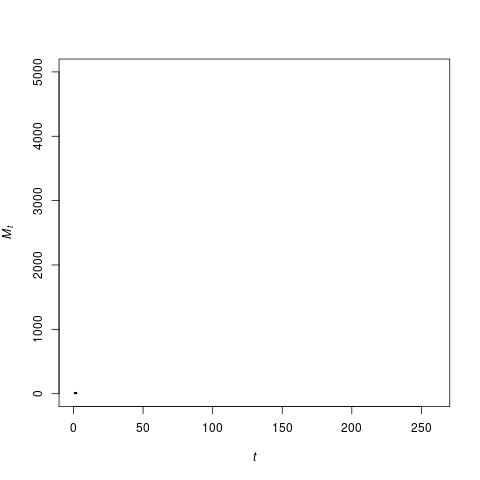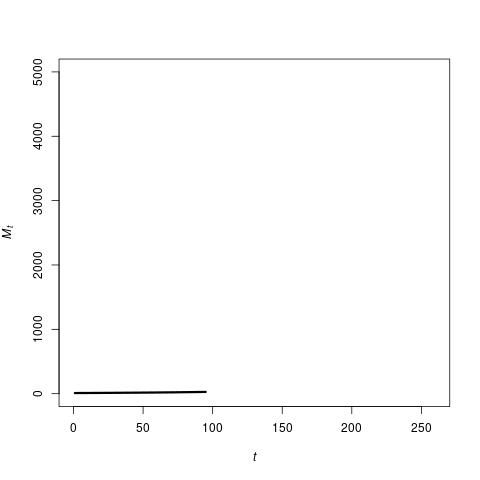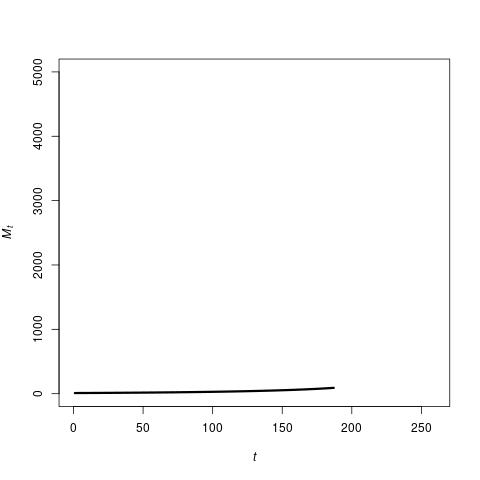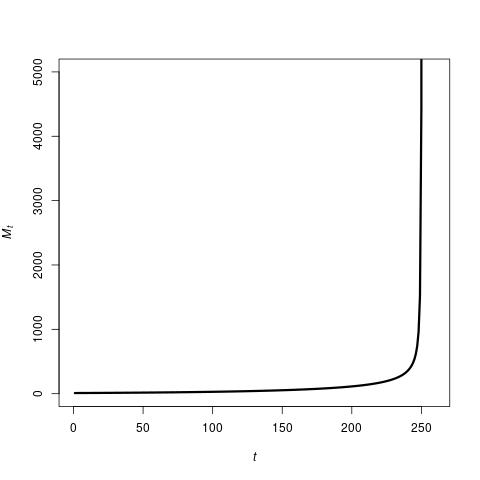
What is most striking here, is that initially there is a long period of very slow growth in the number of technologies Mt, but at some point this rate of growth starts to increase, and very soon after that the number of technologies explodes. In fact, mathematician Mike Steel has shown theoretically that the TAP equation is guaranteed to result in such an explosion. How long it takes to do so depends on the values of the parameters in the model (such as the mentioned probabilities), but given those values it is possible to accurately calculate the expected time to an explosion.
Interestingly, this pattern also occurred with our own technological evolution as outlined earlier. It took millions of years to go from about a dozen or so tools to a few hundred. Then it took hundreds of thousands of years to go from a few hundred tools to a few thousand, and then thousands of years to go from a few thousand to millions, with most of that increase happening in just the last few hundred years.
The TAP equation thus reproduces this actual pattern of technological evolution very closely. However, since it is impossible to know the exact number of technologies that existed at any given time in the past, it is difficult to determine how close the fit between the TAP model and the actual data really is. But there are other ways to express this pattern of technological evolution.
Economic Growth
Technological innovation obviously drives economic growth in general. A standard measure for economic growth is gross domestic product (GDP), which is the monetary value of all final products and services produced and provided within a given country over a certain time period. The image below shows world GDP (i.e., the GDP of all countries combined) per year over the last 2000 years. This measure of economic growth clearly shows the same "hockey stick" pattern, with a very long and slow initial growth, then a sudden acceleration in growth rate, followed by an explosion shortly afterwards.
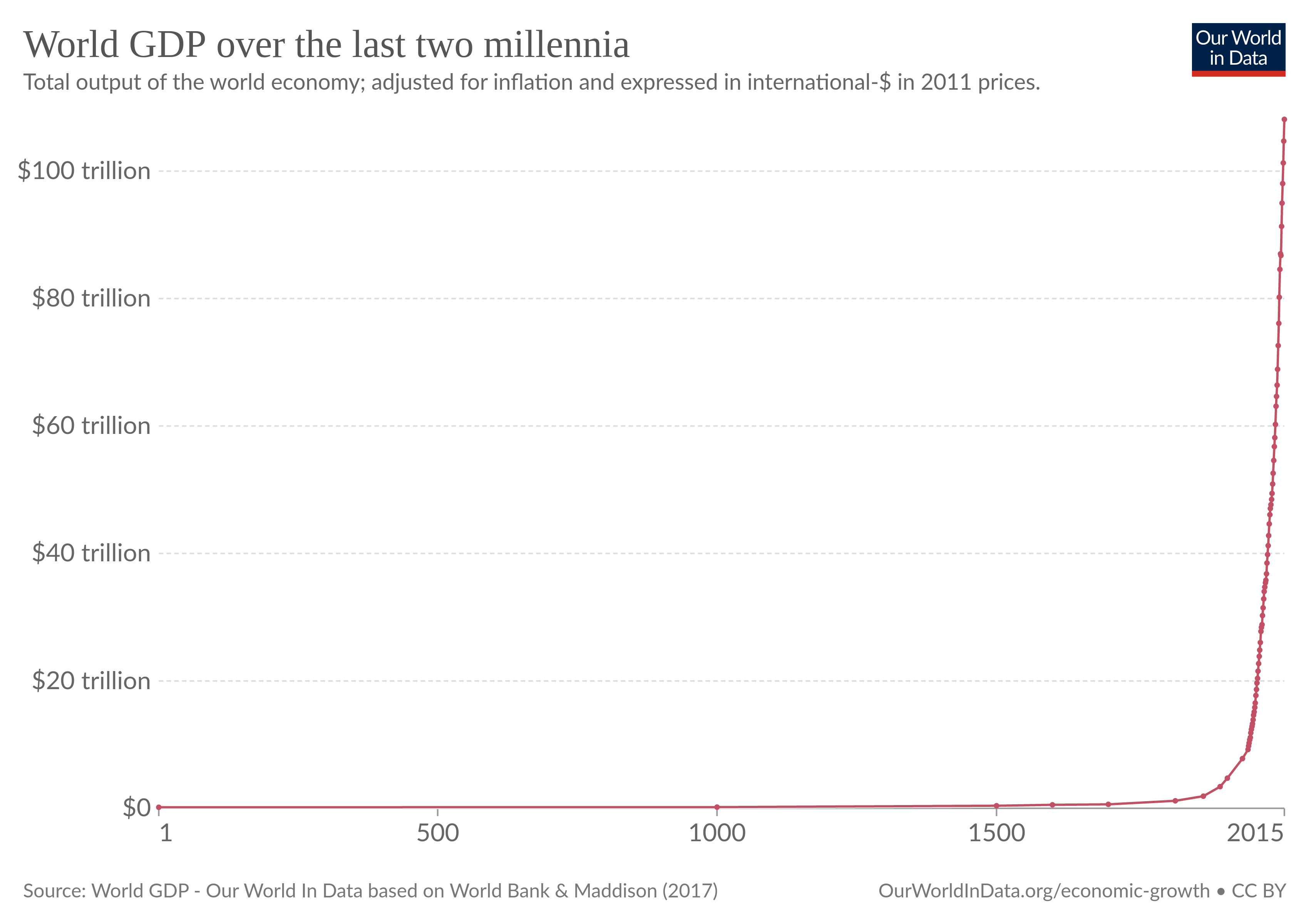
Economist Abigail Devereaux used the TAP equation as input to a standard economic growth model, and after adjusting the parameter values appropriately she was able to fit the model to the world GDP data almost perfectly. Upon seeing these results, Kauffman exclaimed enthusiastically: "TAP fits the data!" Moreover, not only does TAP fit the pattern of technological evolution and economic growth, it also fits a pattern observed in patent data.
Patent Citations
Any patent application cites earlier patents that it builds on. So, for a given patent it is possible to find out what its "children" are, i.e., those patents that cite it directly. Similarly, it is possible to find its "grandchildren", i.e., those patents that cite any of its children, but not directly the patent itself. This way, all the "descendants" (children, grandchildren, great-grandchildren, etc.) of each patent can be determined.
Some patents will only have a few descendants, while others may have very many. This gives rise to a descent distribution: how many patents have one descendant, how many have two, three, a hundred, and so on. Physicist Sergi Valverde reconstructed the descent distribution for several million US patents filed between 1835 and 2010.

It turns out that there are many patents that have just a few descendants, and a few patents that have very many. Such a distribution is mathematically known as a power law. One of the defining characteristics of a power law is its slope, or steepness when visualized in a chart. Valverde found the slope of his patent data to be 1.30. This value happens to fall well within the range predicted by the TAP equation.
By implementing the TAP equation into a computer program, I was able to perform numerical simulations with it. I then also reconstructed the descent distributions from the results of these simulations, just as Valverde had done with the real patent data. Depending on the parameter values used in the TAP equation, I found slopes for the corresponding power laws ranging from 1.10 to 1.35. With a slope of 1.30 as found by Valverde, the TAP equation is clearly able to reproduce the actual patent descent distribution.
The Inevitability of the Anthropocene
In short, the theory of the adjacent possible provides a mathematically precise explanation for technological evolution and economic growth in terms of combinatorial innovation. As such, it gives an alternative explanation for the Anthropocene, and in particular the industrial revolution. Economist Roger Koppl summarized it quite eloquently: "It was not the Protestant ethic, the glorious revolution, British primogeniture, or bourgeois dignity that caused the industrial revolution. It was slow, grinding probability taking its own sweet time before finally delivering the inevitable combinatorial explosion." Indeed, TAP implies there is an inevitability to the Anthropocene.
On the one hand, this technological combinatorial explosion has resulted in better living standards, improved health care, and increased food production. On the other hand, it has also led to overpopulation, environmental pollution, and depletion of resources. So how can this conundrum be resolved? Simply restricting technological innovation might not work. In fact, an alternative version of the TAP equation where existing technologies also have a small probability of "dying" (i.e., they cannot be used to form new technologies anymore) shows that the process then either goes to extinction or still explodes at some point anyway. In other words, it would not continue indefinitely in some intermediate "balanced" state.
Although TAP does not yet give an immediate answer to this difficult question, it does suggest a rethink of how we got here in the first place, and where we might look for potential answers. A further development and investigation of the theory will hopefully provide useful directions for how to deal with the double-edged sword of the Anthropocene, allowing the creative freedom of combinatorial innovation while avoiding an uncontrollable explosion. Much work still lies ahead!